Южанников А.Ю., Южанникова М.А.

Принцип Парето и Золотое сечение

В современной экономике для управления крупными, средними и мелкими предприятиями большинством руководителей принято использовать эмпирическое правило, открытое в 1877 году и названное в честь экономиста и социолога Вильфредо Парето («Принцип Парето» или «Принцип 20/80»). Оно применяется при анализе факторов эффективности деятельности организаций и оптимизации их результатов. В общем виде это правило звучит как «20% усилий дают 80% результата, а остальные 80% усилий – лишь 20% результата». Таким образом, правильно выбрав минимум приоритетных действий, можно получить большую часть запланированного результата, не задействовав при этом всех усилий [1].

Наряду с принципом Парето для поиска оптимального набора прикладываемых усилий применяется принцип «Золотого сечения», который позволяет решить следующую задачу: «в каком соотношении выделить в составе целого некоторые две части так, чтобы они отвечали бы условиям структурной и функциональной целостности и устойчивости единства с внешней средой». Красивый ответ на поставленную задачу дал Леонардо да Винчи в 1509 г, сформулировав правило «Золотого сечения», которое гласит: «Золотое сечение – это такое пропорциональное деление отрезка на две неравные части, при котором длина отрезка так относится к большей части, как большая часть относится к меньшей» [2].

Гармонизация уместна там, где есть структурное разнообразие. «Золотое сечение» можно рассматривать в качестве опорного отношения для гармонизации экономики организаций, состоящих из различных подразделений. Оптимальное (гармонизованное) разнообразие, которое при этом обеспечивается и гарантирует их системное качество, а, следовательно, функциональную эффективность, в результате которой сводится к минимизации непродуктивных (непроизводительных) издержек. Законы Меры, Гармонии, «Золотого сечения» дают возможность строить экономику, суть которой – оптимальное (гармоничное) распределение ресурса [3].

Понятия Меры, Гармонии, «Золотое сечение» пронизывают всю историю науки и культуры. Пирамида Хеопса (Хуфу), самая известная из египетских пирамид, знаменитый Парфенон – храм Афины Парфенос на Акрополе в Афинах, храм Агии Софии в Константинополе, непревзойденная «Джоконда» Леонардо Да Винчи, картины Рафаэля, поэзия А.С. Пушкина и М.Ю. Лермонтова, этюды Шопена, музыка Бетховена и Чайковского, «Модулор» Ле Корбюзье, творения древнерусского зодчества – храм Покрова на Нерли, церковь Вознесения в селе Коломенском – вот не полный перечень выдающихся произведений искусства, наполненных чудесной гармонией, основанной на «Золотом сечении» [4].

Так и в данной работе для исследования мы используем принцип «Золотого сечения», математическая формулировка которого представляется следующим образом:

c :b = b :a, при a + b = c (1)

Графически «Золотое сечение» выглядит как пропорциональное деление отрезка на две неравные части, при котором весь отрезок так относится к большей части, как большая к меньшей (c: b= b: a= 1,618):

Рис.1. Золотое сечение

Известно, что в 1202 г. итальянский математик Леонардо Пизанский, больше известный как Фибоначчи, вывел последовательность чисел, в которой последующее число равно сумме двух предыдущих чисел: 1; 1; 2; 3; 5; 8; 13; 21; 34; 55 и т.д., позднее эта последовательность получила название ряда Фибоначчи [5].

Также Ф = 1,618 является положительным корнем уравнения:

; (2)

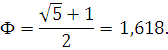
Для обобщенного варианта Золотых р-сечений, предложенного А.П. Стаховым и И.В. Витенько, выведена пропорция:

с :b= (3)

Тогда обобщенное уравнение для Золотых р-сечений выглядит следующим образом:

(4)

Корнями уравнений для Золотых р-сечений при определенных значениях параметра р будут [6]:

Значения корней уравнения для Золотыхр-сечений при разных параметрах р представлены ниже (рис.2) [6]:

a b

р= 0 = 2

р= 1 = 1,618

р= 2 = 1,465

р= 3 = 1,380

р= 4 = 1, 324

р= 5 = 1, 285

р= 6 = 1, 255

р= 7 = 1, 232

… …

р= ∞ = 1

Рис.2 Золотые р-сечения

Следует отметить, что формула для нахождения корня в уравнениях Золотых р-сечений порождает формулу, которая задает бесконечное количество определенных последовательностей, подобных числам Фибоначчи [7]:

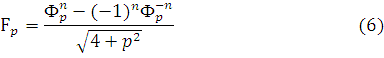
Тогда обобщенные числа Фибоначчи будут иметь следующий вид (таб.1):

Таблица1

Обобщенные числа Фибоначчи

Рр			Порядковый номер числа в последовательности, n
Рр			-5	-4	-3	-2	-1	0	1	2	3	4	5
11	1,618	2,414	5	-3	2	-1	1	0	1	1	2	3	5
22	1,465	3,303	29	-12	5	-2	1	0	1	2	5	12	29
33	1,380	4,236	109	-33	10	-3	1	0	1	3	10	33	109
44	1,324	5,193	305	-72	17	-4	1	0	1	4	17	72	305
55	1,285	6,162	701	-135	26	-5	1	0	1	5	26	135	701
66	1,255	7,140	1405	-228	37	-6	1	0	1	6	37	228	1405
77	1,232	8,123	2549	-357	50	-7	1	0	1	7	50	357	2549

Каждая экономическая система имеет свое структурное разнообразие, которое функционирует на разных уровнях. Для оптимального функционирования любой такой системы с минимум издержек, потерь, непродуктивных энергетических затрат следует придерживаться закону гармонии. Обобщенные «Золотые сечения» суть инварианты, на основе и посредством которых в процессе самоорганизации естественные системы обретают гармоничное строение, стационарный режим существования, структурно-функциональную устойчивость [3].

Что касается принципа Парето, математическая модель для него выглядит таким образом:

a :b = 20 : 80, при. (7)

Графически принцип Парето выглядит как отрезок, поделенный в соотношении 20% на 80% (рис.3):

a b

Рис.3 Принцип Парето

Используя соотношение c: b= 100 : 80,получаем число, равное 1,25.

Возвращаясь к «Золотому сечению», хотели бы воспользоваться одним из его свойств, а именно то, что c:b– 1= a:b. В цифровом виде это выглядит как

1,618 – 1 = 0,618.

По аналогии, применяя это свойство к принципу Парето, мы получим:

c:b– 1= 100 : 80 – 1 = 0,25.

Это есть не что иное, как отношение a:b= 20 : 80 = 0,25.

Исходя из расчетных данных, мы получили, что в принципе Парето корнем уравнения является Ф = 1,25, что близко к значению = 1,255 в «Золотом сечении» (таб.1). Следовательно, можно сделать вывод о том, что принцип Парето является частным случаем «Золотого сечения» при параметре р = 6.

Литература:

1. Кох Р. Принцип 20/80: секреты достижения больших результатов при затрате меньших усилий./ Пер. с англ. – Минск: Попурри, 2004 – 359 с.

2. Иванус, А.И. Код да Винчи в бизнесе или гармоничный менеджмент по Фибоначчи / А.И. Иванус. – Изд. 2-е, испр. – М.: КомКнига, 2006. – 104 с.

3. Сороко, Э.М. Золотые сечения, процессы самоорганизации и эволюции систем. Введение в общую теорию гармонии систем / Э.М. Сороко. – 2-е изд. – М.:КомКнига, 2006. – 264 с.

4. Южанников, А.Ю. Золотое сечение и техноценозы в системах электроснабжения: монография / А.Ю. Южанников. – Красноярск: Поликор, 2009 – 288 с.

5. Воробьев, Н.Н. Числа Фибоначчи / Н.Н. Воробьев. – М.: Наука, 1961. – 144 с.

6. Стахов, А.П. Код да Винчи и ряды Фибоначчи / А.П. Стахов, А.А. Слученкова, И.В. Щербаков. – СПб.: Питер, 2007. – 320 с.

7. Газале, М. Гномон. От фараонов до фракталов / М. Газале перев. с англ. А.Р. Логунова. – М.: Ин-т компьютер. исслед., 2002. – 272 с.